明清之际,西方的数学体系传入中国,中国的学者们在震惊之余,也不断反思,梳理中国古代数学发展的脉络,探究中国古代数学与当时的西方数学间的异同。经过一番研究比较,人们认为,当时的西方数学知识固然先进而自成体系,但其实也是中国"古已有之"的,不足为奇。康熙皇帝时代,"西学中源"说被不少学者认同,他们认为:商高、陈子等人的"勾股术",刘徽的"重差术",就是西方几何学的源头,李冶、朱世杰的"天元术"、"四元术",就是西方代数学的源头,杨辉、朱世杰等人的"垛积术",就是西方微积分的源头,等等。这种思想的形成,无疑源自长期以来中国人"古老而骄傲的"民族性格,我们的古人在数学方面付出了极大的努力,做出了巨大的贡献,让我们不要忘记这些光荣的名字:商高、陈子、刘徽、祖冲之、祖暅、沈括、秦九韶、杨辉、李冶、朱世杰……
十三世纪的宋元时期,中国古代的数学发展又迎来了一个黄金时代,达到了一个新的高峰,可惜这是中国古代数学史上的最后一个高峰,此后,中国古代数学再也没有突破性的进展,而西方的数学研究则取得了飞跃的进步。
在这个最后的黄金时代,中国出现了四位最重要的数学家,被后人称为"宋元四大家",他们是南宋的秦九韶、杨辉,金元时期的李冶,元朝的朱世杰。
1、宋元四大家之秦九韶,
秦九韶,字道古,生于安岳(今四川安岳县)。南宋数学家、官员。代表作《数书九章》18卷(我表示遗憾:北师大版高中数学教材必修5 第51页居然说成《数学九章》!)。
成就:①中国剩余定理(秦九韶定理),比西方的欧拉早500年。它包含在一个称为"大衍总数术"的巧妙算法中。②高次方程的数值解法,比西方的霍纳早500年。③三角形的海伦--秦九韶面积公式(据说这公式阿基米德也已经知道)

2、宋元四大家之李冶
李冶,字仁卿,栾城(今河北栾城县)人,南宋数学家、天文学家、历史学家,进士出身,曾有官职,后归隐封龙山收徒讲学。著有《测圆海镜》、《益古演段》;
其贡献在于引入了名为"天元"(相当于"嫌疑人X")的未知数概念,创立了利用未知数建立方程的方法(天元术),为几何的代数化铺平了道路。此外,李冶还与秦九韶各自独立地引进记号〇表示空位。至此,中国十进制完善了。
3、宋元四大家之杨辉
杨辉,字谦光,临安(今杭州)人,南宋数学家和数学教育家,曾担任地方官。
著有《详解九章算法》、《日用算法》、《杨辉算法》;
成就:发扬光大了沈括、贾宪的数学成就。此外,杨辉还是中国第一个系统研究幻方(Magic square)的人。最早的幻方也出自中国,洛书,又称九宫格。
3、宋元四大家之朱世杰
朱世杰(13世纪末到14世纪初)是中国古代数学家.字汉卿,号松庭,燕山(今北京附近)人,生卒年不详.元统一中国后,他曾以数学家的身份周游各地20余年,向他求学的人很多,他到广陵(今扬州)时"踵门而学者云集".他全面继承了前人数学成果,既吸收了北方的天元术,又吸收了南方的正负开方术、各种日用算法及通俗歌诀,在此基础上进行了创造性的研究,写成以总结和普及当时各种数学知识为宗旨的《算学启蒙》(3卷),又写成四元术的代表作--《四元玉鉴》(3卷),先后于:1299年和1303年刊印.朱世杰是元朝享有盛誉的职业数学家,后人称他"以数学名家,周游湖海二十余年","踵门而学者云集",学术地位非同一般。《算学启蒙》是一部通俗数学名著,曾流传朝鲜、日本等国,古代朝鲜曾以《算学启蒙》开科取士,深刻影响了这些国家的数学教育和发展历史。《四元玉鉴》则是中国宋元时期数学高峰的又一个标志,其中最杰出的数学成就有"四元术"、"垛积术"与"招差术"等。

《算学启蒙》由浅入深,从一位数乘法开始,一直讲到当时的最新数学成果――天元术,形成一个完整体系.书中明确提出正负数乘法法则,给出倒数的概念和基本性质,概括出若干新的乘法公式和根式运算法则,总结了若干乘除捷算口诀,并把设辅助未知数的方法用于解线性方程组.
《四元玉鉴》的主要内容是四元术,即多元高次方程组的建立和求解方法.秦九韶的高次方程数值解法和李冶的天元术都被包含在内.朱世杰的主要贡献是创造了一套完整的消未知数方法,称为四元消法.这种方法在世界上长期处于领先地位,直到18世纪,法国数学家贝祖(Bezout)提出一般的高次方程组解法,才超过朱世杰.除了四元术以外,《四元玉鉴》中还有两项重要成就,即创立了一般的高阶等差级数求和公式及等间距四次内插法公式,后者通常称为招差术.此书代表着宋元数学的最高水平,美国科学史家萨顿(G.Sarton)称赞它"是中国数学著作中最重要的一部,同时也是中世纪的杰出数学著作之一."
朱世杰处于中国传统数学发展的鼎盛时期.当时社会上"尊崇算学,科目渐兴",数学著作广为传播.在宋元时期的数学群英中,朱世杰的工作具有特殊重要的意义.如果把诸多数学家比作群山,则朱世杰是最高大、最雄伟的山峰.站在朱世杰数学思想的高度俯嫩传统数学,会有"一览众山小"之感.来世杰工作的意义就在于总结了宋元数学,使之在理论上达到新的高度.这主要表现在以下三个领域.

首先是方程理论.在列方程方面,蒋周的演段法为天元术作了准备工作,他已具有寻找等值多项式的思想,洞渊马与信道是天元术的先驱,但他们推导方程仍受几何思维的束缚,李冶基本上摆脱了这种束缚,总结出一套固定的天元术程序,使天元术进入成熟阶段.在解方程方面,贾宪给出增乘开方法,刘益则用正负开方术求出四次方程正根,秦九韶在此基础上解决了高次方程的数值解法问题.至此,一元高次方程的建立和求解都已实现.而线性方程组古已有之,所以具备了多元高次方程组产生的条件.李德载的二元术和刘大鉴的三元术相继出现,朱世杰的四元术正是对二元术、三元术的总结与提高.由于四元已把常数项的上下左右占满,方程理论发展到这里,显然就告一段落了.从方程种类看,天元术产生之前的方程都是整式方程.从洞渊到李冶,分式方程逐渐得到发展.而朱世杰,则突破了有理式的限制,开始处理无理方程.
案例:天元术以"元"代表未知数X,以"太"代表常数项。列式时把元字写在算码的右侧,如11元即表示2x,或单写太,如11太也同。写了元便不写太,写了太便不写元。方程式的各项是从下而上,即太在元下,太是常数项,元是X项,元上是X2项,再上是X3项等等。太下是1/X(即X-1)项,再下是X-2项等等。也有记法从上而下恰恰相反。在用算筹排列时,正数用红色筹。负数用黑色筹。用算码时,正负数也用红黑色区别,但为了书写方便,可在算码的个位数加一斜撇,如-2作■,-231作‖川卜。天元术的方法一般是根据问题中已有条件,立天元一(x)为未知数(所求数),最后列出方程式,解方程得数。至于解方程式在一元三次以上,就要用到贾宪的方法。

其次是高阶等差级数的研究.沈括的隙积术开研究高阶等差级数之先河,杨辉给出包括隙积术在内的一系列二阶等差级数求和公式.朱世杰则在此基础上依次研究了二阶、三阶、四阶乃至五阶等差级数的求和问题,从而发现其规律,掌握了三角垛统一公式.他还发现了垛积木与内插法的内在联系,利用垛积公式给出规范的四次内插公式.
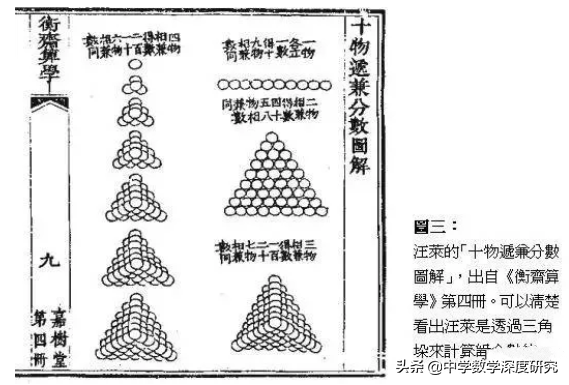
第三是几何学的研究.宋代以前,几何研究离不开勾股和面积、体积.蒋周的《益古集》也是以面积问题为研究对象的.李冶开始注意到圆城因式中各元素的关系,得到一些定理,但未能推广到更一般的情形.朱世杰不仅总结了前人的勾股及求积理论,而且在李冶思想的基础上更进一步,深入研究了勾股形内及圆内各几何元素的数量关系,发现了两个重要定理--射影定理和弦幂定理.他在立体几何中也开始注意到图形内各元素的关系.朱世杰的工作,使得几何研究的对象由图形整体深入到图形内部,体现了数学思想的进步.

由此看来,在朱世杰的工作中,不仅有高次方程的解法,天元术等为代表的北方数学的成就,也包括了杨辉工作中所体现出来的日用,商用算法以及各种歌诀等南方数学的成就,不仅继承了中国古代数学的光辉遗产,而且又作了创作性的发展。朱世杰的工作,在一定意义上讲,可以看作是宋元数学的代表,可以看作是古代筹算系统发展的顶峰。就连西方资产阶级学者们也不能否认这一点,乔治萨顿说:朱世杰"是汉族的,他所生存的时代的,同时也是贯穿古今的一位最杰出的数学家",说《四元玉鉴》"是中国数学著作中最重要的一部,同时也是中世纪最杰出的数学著作之一"。朱世杰以他自己的杰出著作,把中国古代数学推向更高的境界,为中国古代数学的光辉史册,增加了新的篇章,形成了宋代中国数学发展的最高峰。
